Nonlinear transform coding using neural networks

Undergraduate thesis project on compressing CT scans using neural networks.

Thesis Slides

Standard lossy image compression techniques rely on linear transform coding, which leverages orthogonal transformations to decorrelate and compress an image. Nonlinear transform coding offers a more versatile option capable of achieving better decorrelation (and therefore, better performance).

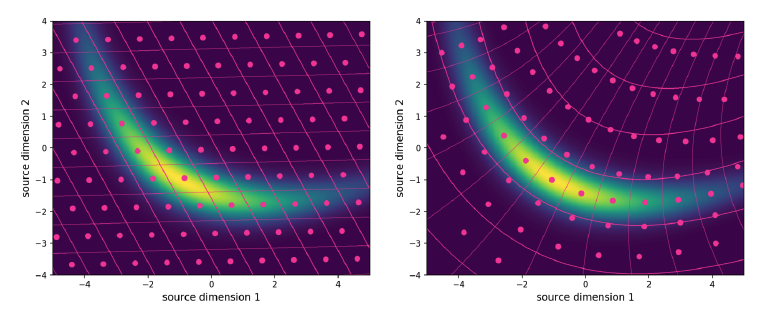
Comparison of linear transform coding (left) and nonlinear transform coding (right) for a banana-shaped distribution. Lines indicate quantization bins, with dots the codebook vectors. Image credit Ballé et al. "Nonlinear Transform Coding," (Oct 2020).

This project mathematically formulates a nonlinear transform coding system as a pair of analysis and synthesis transforms, each parametrized by a neural network. The end-to-end system is trained to compress CT scans, an application of particular importance to low-bandwidth areas without easy access to health care services. A custom loss function is used to balance the distortion (difference) between the original and compressed image with the rate (size) of the compressed image. This project was implemented in Python, using Tensorflow for the neural networks.

Our thesis won the 2023 Keyser Prize, which recognizes the best thesis of the Mathematics and Engineering program.